Einige Sätze über Primzahlen
und spezielle binomische Ausdrücke
Hans Walther Ernst Gerhart Schmidt
Zweite Fassung 19.08.2015
Hauptstraße 33, D-04668 Otterwisch, Germany
hws@schmidt-guetter.de
Schlüsselwörter: Primzahlen, Gauß-Legendre-Theorem, Goldbach, Lücken, Vierlinge, Zwillinge
Dieser Artikel ist lizensiert als Inhalt der Creative Commons Namensnennung - Nicht-kommerziell - Weitergabe unter gleichen Bedingungen 4.0 Unported-Lizenz. Um eine Kopie der Lizenz zu sehen, besuchen Sie http://creativecommons.org/licenses/by-nc-sa/4.0/ .
1. There is no existing any quadratic interval ηn: = (n2, (n + 1)2], which contains less than 2 prime numbers.
The number of prime numbers within ηn goes averagely linear with n to infinity.
2. The exact law of the number π(n) of prime numbers smaller or equal to n is given. As an approximation of that we get the prime number theorem of Gauss for great values of n.
3. We derive partition laws for π(ηn), for the number of twin primes π2(ηn) in quadratic intervals ηn and for the multiplicity πg(2n) of representations of Goldbach-pairs for a given even number 2n similiar to the theorem of Gauss.
4. There is no natural number n>7, which is beginning point of a prime number free interval with a length of more than 2*SQRT(n).
5. It follows, that the number of twin primes goes to infinity as well as the number of Goldbach-pairs for a given 2n, if n goes to infinity.
6. Besides this our computation gives a new proof for the prime number theorem of Gauss.
\selectlanguagegerman
1 Einleitung
Durch die Fach- und sogar Tagespresse huschen in den letzten Jahren gelegentlich neue Rekordmeldungen über Primzahlen, wie etwa: ”...neue, bisher größte Primzahl gefunden mit Hilfe eines Supercomputers...” oder: ”...bisher größter Primzahlzwilling entdeckt...”. Solche Aussagen haben geringen wissenschaftlichen Wert, da sie im allgemeinen keine Informationen über verwendete Entscheidungsalgorithmen enthalten. Auch stellen sie keine Hilfe zur Entscheidung der Fragen dar, ob die Menge der Primzahlzwillinge, der Fermat’schen oder Mersenneschen Primzahlen endlich ist oder nicht. Nachfolgend soll gezeigt werden:
- Es wird eine exakte Formel angegeben zur Berechnung der Anzahl π(x) von Primzahlen ≤ x, aus der sich der Primzahlsatz von Gauß und Legendre als Näherung für große x ergibt.
- Da auch analoge Gesetze für die Anzahlen π(ηn) von Primzahlen in Quadratintervallen ηn: = (n2, (n + 1)2], für die Anzahl von Primzahlzwillingen π2(ηn) und die Vielfachheit von Goldbachpaar-Darstellungen πg(2n) für eine vorgelegte gerade Zahl 2n ableitbar sind, kann gezeigt werden, daß alle diese Größen für n → ∞ über alle Grenzen wachsen. Solches gilt vermutlich sogar für Primzahlvierlinge in biquadratischen Intervallen oberhalb eines Schwellwertes.
Zuerst sollen im 2. Kapitel einige allgemein bekannte Beziehungen über die Teilbarkeit von Binomina der Form z± = 2x±1 zusammengestellt werden. Die Kapitel 3 und 4 der ersten Fassung dieses Artikels sind gegenstandslos geworden. Das 5. Kapitel liefert eine exakte Darstellung für π(x), woraus der Gauß’sche Primzahlsatz als Näherung abgeleitet wird, und die Primzahlverteilung über Quadratintervallen. Im 6. Kapitel wird eine obere Schranke für die maximale Länge des einer natürlichen Zahl n folgenden primzahlfreien Intervalls angegeben. Im 7., 8. und 9. Kapitel folgen die Anwendungen auf π2(ηn), die Vierlingsanzahl π4(n4) und πg(2n). Die abgeleiteten Streubreiten der π-Funktionen werden im Anfangsbereich mit numerisch-experimentellen Befunden verglichen.
2 Teilbarkeitsbeziehungen für Binomina der Form
z± = 2x±1
Satz 2.1. Jede natürliche Zahl a < ∞, aϵℕ, hat die kanonische Primfaktorzerlegung
n0= Anzahl der von einander verschiedenen Primfaktoren, ni ihre jeweilige Vielfachheit, oder
unter Verwendung aller Primzahlen in ihrer natürlichen Reihenfolge, worin alle ni = 0 erfüllen, die nicht in (1↑) auftreten. Faßt man hierin alle ungeraden Primfaktoren in
m = n0∏i = 2pnii
zusammen, so ergibt sich a = 2n1m. Für n1 = 0 ist a = m ungerade. Jede ungerade Zahl m hat auch eine Darstellung
Satz 2.2. Die Summe m aus zwei beliebigen natürlichen Zahlen ist genau dann eine ungerade Zahl (n1 = 0), wenn genau einer der Summanden ungerade ist:
(4) s = a1 + a2 = 2n1m1 + 20m2 = m.
Das Produkt aus zwei natürlichen Zahlen a1a2 kann nur ungerade sein, wenn a1und a2 ungerade sind.
Satz 2.3. Aus dem allgemeinen Binomischen Satz
ergibt sich für a=b=1 und m=ungerade natürliche Zahl
weil (mν) = (mm − ν) gilt. Für eine gerade Zahl m = 2l ergibt sich
mit dem binomischen Koeffizienten
2B = 2B2l − 1, l − 1 = B2l, l = (2ll) = (m(m)/(2)).
Wählt man eine ungerade Primzahl p ≥ 3 für m, so gilt außer Bm, ν = (mν) = Bm − ν, ν = (m − νν), daß in jedem Binomialkoeffizienten mit 0 < ν < m der größte Faktor im Zähler gleich p ist, also ausgeklammert werden kann, da er als Primzahl gegen keinen Nennerfaktor, die alle kleiner sind, zu kürzen ist:
oder
(9) 2p − 1 = 1 + 2pM
sowie
(10) 2p + 1 = 3 + 2pM .
Aus (9↑) folgt 2p − 1 − 1 = pM = 3pM’ nach (18↓), sodaß (10↑) auch als 2p + 1 = 3(1 + 2pM’) geschrieben werden kann. Stets gilt dann 2p − 1 ≡ 1mod3, 2p + 1 ≡ 0mod3.
Satz 2.4. Sei p > 2 eine Primzahl, m > 1 eine ungerade natürliche Zahl. Dann gelten mit N± > 1
Bew.: Man wähle in Satz 2.3. für m ein m’ = pm. Mit den Abkürzungen L = 2p − 1 , M = 2p + 1 kann geschrieben werden
2pm − 1 = (L + 1)m − 1 = m⎲⎳ν = 0Bm, νLm − ν − 1 = LN −
mit N − = ∑m − 1ν = 0Bm, νLm − 1 − ν > 1. Analog folgt mit N + = ∑m − 1ν = 0Bm, ν( − 1)νMm − 1 − ν sodann 2pm + 1 = (M − 1)m + 1 = ∑m − 1ν = 0Bm, ν( − 1)νMm − ν = MN + , q.e.d.
Bemerkung 2.4.1. Es gilt Satz 2.4. für jeden Teiler pi von m’ = a nach (1↑). Daraus folgt aber
nur, wenn Teilerfremdheit (2pi±1)∤(2pj±1)∀i, j ≤ n0 gezeigt ist. Andernfalls tritt ein Teiler pk\(2pi±1) im Ausdruck für 2m’±1 nur höchstens in der Potenz auf, in der er in einem der Teilerbinomina vorkommt: pnkk\(2pi±1). Das Beispiel 23⋅11 + 1 = 32⋅67⋅683⋅20857 ≠ (23 + 1)(211 + 1)N + = (32)(3⋅683)N + zeigt, daß der Faktor pk = 3 nicht in 3., sondern nur in 2. Potenz in der Faktorisierung auftritt.
Bemerkung 2.4.2. Während (11↑) auch für p1 = 2 gilt, ist dies bei (12↑) nicht der Fall, was aus dem folgenden Satz hervorgeht.
Satz 2.5. . Seien i, m natürliche Zahlen, m > 1 ungerade. Dann gilt ∀i, m mit den Fermat-Zahlen Fν = (2(2ν) + 1) und Mν > 1, ungerade,
(15) 2m2i + 1 = FiMi
mit Mi > 1; nur für m = 1 folgt Mi = 1. Dabei kann (2m − 1) noch nach Satz 2.4. weiter aufgespaltet werden. Falls m = pjm’ gilt, kann etwas allgemeiner statt (15↑) geschrieben werden:
Bemerkung 2.5.1.: Wegen 20 = 1 gilt ∀m ungerade
(17) 2m + 1 = 2m20 + 1 = 3M0.
Weil für jede gerade Zahl g gilt
folgt 3\(2g − 1) ∀g.
Bew.: ad (15↑) :
2m2i + 1
=
[2(2i) + 1 − 1]m + 1 = 1 + m⎲⎳ν = 0Bm, ν( − 1)ν[2(2i) + 1]m − ν
=
FiMi mit Mi = m − 1⎲⎳ν = 0( − 1)νBm, νFm − 1 − νi.
(16↑) ergibt sich analog, indem im ersten Schritt nur [⋯]m’oder [⋯]p gebildet wird. Für m > 1 folgt stets Mi > 1 wegen
2m2i + 1 = [2(2i)]m + 1 > 2(2i) + 1.
ad (14↑):
2m2i − 1
=
(2m2i − 1 + 1)(2m2i − 1 − 1) = ⋯
=
(2m − 1)i − 1∏ν = 0(2m2ν + 1) = (2m − 1)i − 1∏ν = 0FνMν.
Hierin tritt das Produkt aller Fermat-Zahlen mit ν = 0(1)i − 1 auf, weil jede Fermat-Zahl Fi teilerfremd ist zu allen Fν mit ν < i (siehe folgender Satz); q.e.d.
Satz 2.6. Folgende Ausdrücke sind zueinander teilerfremd: a)
b) die Fermatzahlen
(20) Fi∤Fj ∀j < i.
Bew.: ad a) Wegen (2i + 1) − (2i − 1) = 2 ist der größte gemeinsame Teiler ≤ 2. Da ∀i > 1 gilt 2i±1≥3 ungerade, kann nur eine ungerade Zahl ≥3 gemeinsamer Teiler sein. Die Menge der gemeinsamen Teiler ist also leer, es gilt a).
ad b) Es ist Fi − 1(Fi − 1 − 2) = (2(2i − 1) + 1)(2(2i − 1) − 1) = 2(2i) − 1 = Fi − 2. Dann folgt Fi − 1 = (Fi − 2)/(Fi − 1 − 2) und ∏i − 1ν = 0Fν = (Fi − 2)/(Fi − 1 − 2)⋅(Fi − 1 − 2)/(Fi − 2 − 2)⋅…⋅(F1 − 2)/(F0 − 2) = Fi − 2 nach Kürzung, da F0 − 2 = 1, also gilt b) ; q.e.d.
Aus dem bisher Ausgeführten geht hervor, daß als Primzahlanwärter nur die Mersenne-Zahlen Mp = 2p − 1 und die Fermat-Zahlen Fi = 2(2i) + 1 in Betracht kommen. Alle anderen z± = (2x±1) sind als teilbar erwiesen. Es wäre daher wünschenswert, die Primzahl-Anwärterzahlen aufgrund von Exponenteneigenschaften allein in prime und teilbare Zahlen klassifizieren zu können, zumal unter den Anwärtern nur wenige echte Primzahlen enthalten sind.
Eine weitere Klasse teilbarer Zahlen definiert
Satz 2.7. Es sei gemäß der kanonischen Primzahlzerlegung (1↑) n = ∏∞i = 1pαii = m2α1 mit m > 1, ungerade, und p’ = 2n + 1 > 3 eine ungerade Primzahl. Dann gilt
Bemerkung 2.7.1: Insbesondere impliziert (22↑) für (p’ − 1)/(2) = n = m = p ≡ − 1mod4 die Teilbarkeit der Mersennezahl Mp, also
sowie (23↑) für (p’ − 1)/(2) = n = m = p ≡ + 1mod4, daß
gilt. (Den Beweis, daß p’\(2p − 1) gilt, g.d.w. p’ = 2p + 1 und p ≡ 3mod4 gilt, s. [1], p.174, Satz 21 mittels quadratischen Kongruenzen.)
Bemerkung 2.7.2. Ist n = pim ≡ ±1mod4, so folgt unter Berücksichtigung von (11↑), (12↑)
Ob darin p’\(2pi±1) gilt oder p’\Ni, ± , bleibt zunächst offen.
Bew.: Mit p’ statt p in (9↑) folgt unter Beachtung der Bemerkung zu Satz 2.5. und mit p’ − 1 = 2n = m21 + α
n = (p’ − 1)/(2) = m2α. Darin ist stets
(29) 2n + 1 = 2m2α + 1 = FαMα
nichtprim mit Fα = (2(2α) + 1), Mα > 1∀m > 1; nur für m = 1 ist Mα = 1 und Fα Primzahlanwärter; sowie
Die Folge der Fermat’schen Primzahlen beginnt mit
(31) {Fν} = {3, 5, 17, 257, 65537, …}.
Ist m teilbar, etwa pj\m, so gilt zusätzlich (2m − 1) = (2pj − 1)Nj − nichtprim.
a) Zuerst sei α = 0 angenommen. Dann ist n = m ≥ 3 und p’ = 1 + 2m. Mithin gilt für m mod 8 ≡ 1 oder 5 (d.h. m mod 4 ≡ 1 ), daß p’ ≡ 3 mod 8 und für m mod 8 ≡ 3 oder 7 (d.h. m mod 4 ≡ − 1 ), daß p’ ≡ 7 mod 8. Es sei nun m = p als Primzahl angenommen und
1.) p’ = 1 + 2p ≡ 3 mod 8, also p mod 8 ≡ 1 oder 5, d.h. p mod 4 ≡ 1. Nimmt man weiter unter dieser Voraussetzung an, daß p’\(2p − 1) gilt, so folgt hieraus unter Beachtung von (9↑), (10↑), (17↑), (18↑), 2p − 1 = 1 + 2⋅3pM’1 ≡ 7 mod 8 und weiter 2p − 1 − 1 = 3pM’1 ≡ 7 mod 8, also pM’1 ≡ 5 mod 8, sowie 2p + 1 = 3(1 + 2pM’1) ≡ 1 mod 8 und weiter 1 + 2pM’1 ≡ 3 mod 8, also pM’1 ≡ 1 mod 8 im Widerspruch zur vorigen Zeile. Mithin ist die Annahme p’\(2p − 1) falsch. Da die Annahme (3p’)\(2p + 1) wegen 3p’ ≡ 1 mod 8 keinen Widerspruch liefert, ist (23↑) bewiesen für m = p.
2.)Sei p’ = 1 + 2p ≡ 7 mod 8, also p mod 8 ≡ 3 oder 7 bzw. p mod 4 ≡ − 1. Sei weiter angenommen, daß p’\(2p + 1) gilt, so folgt daraus 2p + 1 = 3 + 2⋅3pM’1 ≡ 1 mod 8, also 2p − 1 − 1 = 3pM’1 ≡ 7 mod 8, also pM’1 ≡ 5 mod 8. Andererseits folgt aus 2p + 1 = 3(1 + 2pM’1) ≡ 1 mod 8, also 1 + 2pM’1 ≡ 3 mod 8, der Widerspruch pM’1 ≡ 1 mod 8. Daher gilt (22↑) für m = p.
b) Im Falle α = 1 gilt p’ = 1 + m21 + α = 1 + 4m ≡ 5 mod 8 ∀m , n = (p’ − 1)/(2) = 2m und wegen 24m − 1 = (22m + 1)(22m − 1) = p’M = 3p’M’. Darin ist 22m + 1 = F1M1 mit F1 = 5, M1 ≡ 5 mod 8 und 22m − 1 = (2m + 1)(2m − 1) mit 2m + 1 = F0M0, F0 = 3, M0 ≡ 3 mod 8, und 2m − 1 = (2pj − 1)Nj − ≡ (2pj − 1) ≡ 22m − 1 ≡ 7 mod 8, Nj − ≡ 1 mod 8. Nun gilt 3\(22m − 1), 3\(2m + 1), 3∤(2m − 1), 3∤(22m + 1). Es ist 22m + 1 ≡ 52 mod 8 und 22m − 1 = (2m + 1)(2m − 1) ≡ (32 mod 8)⋅(7 mod 8), worin kein Faktor ≡ 5 mod 8, also kein p’ vorkommt. Deshalb kann p’ ≡ 5 mod 8 nur Teiler von (22m + 1) sein, also gilt (24↑) mit n = 2m. (Sollte nämlich in 2m − 1 ein Faktor ≡ 5 mod 8 enthalten sein, so müßte auch ein Faktor ≡ 3 mod 8 darin möglich sein, damit ≡ 7 mod 8 entsteht. Der Faktor ≡ 3 mod 8 tritt aber in 2m + 1 auf, das teilerfremd zu 2m − 1 ist.)
c) Im Falle α ≥ 2 gilt schließlich 1 + m21 + α ≡ 1 mod 8 ∀m, (p’ − 1)/(2) = n = m2α. Statt (28↑) haben wir dann
2p’ − 1 − 1 = 22n − 1 = p’M = 3p’M’ = (2n + 1)(2n − 1) = (2m − 1)α∏ν = 0FνMν,
worin 2n + 1 = FαMα mit Fα ≡ Mα ≡ 1 mod 2(2α) ∀α ≥ 2 und
2n − 1 = (2pj − 1)Nj − ⋅3M0⋅5M1α − 1∏ν = 2FνMν
mit ∏1ν = 2FνMν = 1 für α = 2. Darin bezeichnet pj einen beliebigen Teiler von m, für den Satz 2.4. die angegebene Darstellung garantiert.
Es kann nun p’\(2n + 1) nicht gelten, weil beide angegebenen Faktoren ≡ 1 mod 2(2α) erfüllen, während p’ = 1 + m21 + α ≡ 1 mod 21 + α nur erfüllt mit 21 + α < 2(2α)∀α > 2. Daß für α = 2 gilt 21 + α = 2(2α), stört nicht, weil m > 1 vorausgesetzt ist. Dann muß also (21↑) gelten; q.e.d.
Ob der Teiler p’ nun p’\(2m − 1) = (2pj − 1)Nj − mit Nj − ≡ 1 mod 8 erfüllt oder p’\FνMν, Fν ≡ Mν ≡ 1 mod 8, bleibt offen.
3 Eine unendliche Folge Fermat’scher Primzahlen
Die Kapitel 3 und 4 der ersten Fassung dieses Artikels sind fehlerhaft und werden als gegenstandslos gestrichen, denn nach privater Mitteilung von D.Eschbach gibt es in der Literatur Gegenbeispiele, s.a. http://www.prothsearch.net/fermat.html.
4 Unendliche Folgen Mersennescher Primzahlen
5 Exakte Bestimmung der Anzahl der Primzahlen unterhalb einer vorgegebenen Schranke
5.1 Vorbereitende Bemerkungen
In Analogie zur Fakultätsfunktion n! = ∏ni = 1i wird die Primfakultät , in Zeichen pi↓, erklärt durch Def. 5.1:
(32) pn↓ = n∏i = 1pi ,
wobei pi das i-te Element in der natürlichen Folge der Primzahlen {pi} bedeutet.
Def. 5.2. Es sei x eine beliebige reelle Zahl. Dann bezeichne [x] die größte ganze Zahl, die noch kleiner oder gleich x ist, und ≺x≻ sei die größte Primzahl, die ≤ x ist.
Bemerkung 5.2.1. Stets gilt
Def. 5.3. Es bezeichne Ci, m, k das zahlenmäßige Produkt aller Elemente der k-ten Kombination von i Elementen ohne Wiederholungen. Der Index k soll keine Ordnung der Kombinationen, sondern lediglich deren Unterscheidbarkeit und somit Numerierbarkeit bewirken. Es gelte
(34) C0, m, k = 1 ∀m, k,
d.h. eine Kombination aus i = 0 Elementen soll den Faktor 1, die multiplikative Invariante, ergeben.
Bemerkung 5.3.1. Die über k summierte Anzahl B der Kombinationen Cj, i − 1, k ergibt einen binomischen Koeffizienten
Dann soll abkürzend geschrieben werden:
Bemerkung 5.3.2. Es gilt
Def. 5.4. Es sei x eine beliebige positive reelle Zahl. Dann bezeichne i0 den durch
(38) pi0 = ≺√(x)≻
definierten zugehörigen Index in der natürlichen Folge der Primzahlen.
Lemma 5.1. Seien {a, b} reelle Zahlen, a = [a] + ϵa, b = [b] + ϵb, 0 ≤ ϵa, b < 1. Dann
gilt
a ≥ [a], [ − ∣a∣] ≤ − ∣a∣ ≤ − [∣a∣] ≤ 0,
für a < 0 ist [ − ∣a∣] = [a] und [ − a] = [∣a∣];
Bew.: Die Beziehungen (39↑) entsprechen der Definition 5.2. , woraus ebenfalls folgt a + b ≥ [a + b] = [[a] + ϵa + [b] + ϵb] = [a] + [b] + [εa + εb] ≥ [a] + [b], weil [a] und [b] als ganzzahlige Größen ohne Wertänderung aus der Summe in der äußeren eckigen Klammer herausgezogen werden können und 0 ≤ εa + εb < 2 gilt, womit die erste Formel (40↑) gezeigt ist. Die zweite Ungleichung unter (40↑) folgt aus der ersten mit a’ = a − b, also a ≥ [a] = [a − b + b] = [a’ + b] ≥ [a − b] + [b]. Die dritte Ungleichung ist eine Umstellung der zweiten. Wegen [a] = [a − ∑i bi + ∑i bi] ≥ [a − ∑i bi] + [∑i bi] ≥ [a − ∑i bi] + ∑i[bi] folgt sofort (41↑). Ersetzt man in (40↑) a durch a’ = ∣a∣ und b durch b’ = − ∣b∣, so folgt (42↑) mit Hilfe von (39↑); q.e.d.
Lemma 5.2. Seien {a, b} reelle Zahlen, {c, n} natürliche Zahlen. Es gelte ∣a∣ ≥ ∣b∣ und a ≠ nbc. Dann gilt für c = 1
(a)/(bc) ≥ (1)/(c)⎡⎣(a)/(b)⎤⎦ = ⎡⎣(a)/(bc)⎤⎦ = ⎡⎣(a)/(b)⎤⎦
sowie ∀c > 1
(43) (a)/(bc) ≥ (⎡⎣(a)/(b)⎤⎦)/(c) ≥ ⎡⎢⎣(⎡⎣(a)/(b)⎤⎦)/(c)⎤⎥⎦ = ⎡⎣(a)/(bc)⎤⎦ ≥ ⎡⎣(1)/(c)⎤⎦⎡⎣(a)/(b)⎤⎦ = 0
sowie
Bew.: Die Aussage für c = 1 ist trivial wegen ⎡⎣(1)/(c)⎤⎦ = (1)/(c) = 1, weswegen auch (44↑) für c = 1 auf 0 = 0 führt. Für c > 1 gilt wegen (a)/(b) = ⎡⎣(a)/(b)⎤⎦ + ε mit 0 ≤ ε < 1 und [a] ≤ a = nab + rb , 0 ≤ rb < b, (a)/(b) = (nab + rb)/(b) = na + (rb)/(b) mit na = ⎡⎣(a)/(b)⎤⎦, 0 ≤ (rb)/(b) = εb < 1. Es enthält na stets das Vorzeichen von (a)/(b) , welches in der [⋅] bleiben muß und nicht etwa mit der als positiv vorausgesetzten Konstante c herausgezogen werden darf. Nach Division durch c ergibt sich
(a)/(bc) = (na)/(c) + (rb)/(bc) = nc + (rc)/(c) + (rb)/(bc) = nc + (1)/(c)⎛⎝rc + (rb)/(b)⎞⎠
mit 0 ≤ rc ≤ c − 1, also 0 ≤ rc + (rb)/(b) < c, sodaß nc = ⎡⎣(a)/(bc)⎤⎦, 0 ≤ εbc: = (rc)/(c) + (rb)/(bc) < 1 gilt. Dann hat man
(45) ⎡⎣(a)/(bc)⎤⎦ = ⎡⎢⎣(⎡⎣(a)/(b)⎤⎦)/(c) + (rb)/(bc)⎤⎥⎦ = ⎡⎢⎣⎡⎢⎣(⎡⎣(a)/(b)⎤⎦)/(c)⎤⎥⎦ + (rc)/(c) + (rb)/(bc)⎤⎥⎦ = ⎡⎢⎣(⎡⎣(a)/(b)⎤⎦)/(c)⎤⎥⎦
als ganzzahligen Anteil aus der dritten eckigen Klammer, deren gebrochener Teil unterdrückt werden soll. Dann folgt
(a)/(bc) ≥ (⎡⎣(a)/(b)⎤⎦)/(c) ≥ ⎡⎢⎣(⎡⎣(a)/(b)⎤⎦)/(c)⎤⎥⎦ = ⎡⎣(a)/(bc)⎤⎦ ≥ ⎡⎣(1)/(c)⎤⎦⎡⎣(a)/(b)⎤⎦ = 0,
also (43↑), und daraus − ⎡⎣(a)/(bc)⎤⎦ ≥ − (1)/(c)⎡⎣(a)/(b)⎤⎦, was nach Addition von ⎡⎣(a)/(b)⎤⎦ gerade (44↑) ergibt; q.e.d.
Lemma 5.3. Mit den Bezeichnungen aus Definition 5.3. gilt unter Beachtung der Bemerkungen 5.3.1. und 5.3.2.
und
Bew.: Die linke Seite von (46↑) ergibt sich bei sukzessiver Berechnung des Produktes der rechten Seite: Für i = 1 hat man nach Definition
0∏j = 0⎛⎝1∓(1)/(pj)⎞⎠ = 1,
i = 2:
1∏j = 1⎛⎝1∓(1)/(pj)⎞⎠ = 1∓(1)/(p1) = \Bigl{1 ⁄ 2\atop3 ⁄ 2 ,
i = 3:
2∏j = 1⎛⎝1∓(1)/(pj)⎞⎠ = ⎛⎝1∓(1)/(p1)⎞⎠⎛⎝1∓(1)/(p2)⎞⎠ = i − 1⎲⎳j = 0 ⎲⎳∀k((±1)j)/(Cj, i − 1, k) = \Bigl{1 ⁄ 3\atop2 .
Induktionsvoraussetzung: Die Formel gilt ∀i ≤ i0 − 1 = 2. Dann gilt für i = i0:
i0 − 1∏j = 1⎛⎝1∓(1)/(pj)⎞⎠
=
⎛⎝1∓(1)/(pi0 − 1)⎞⎠i0 − 2∏j = 1⎛⎝1∓(1)/(pj)⎞⎠
=
⎛⎝1∓(1)/(pi0 − 1)⎞⎠i0 − 2⎲⎳j = 0 ⎲⎳∀k((±1)j)/(Cj, i0 − 2, k) = i0 − 1⎲⎳j = 0 ⎲⎳∀k((±1)j)/(Cj, i0 − 1, k);
q.e.d.
5.2 Die Anzahl echt teilbarer natürlicher Zahlen ≤ x
Die Zahl 1 gehört als multiplikative Invariante nicht zu den Primzahlen, denn sie kann in beliebiger ganzzahliger Potenz einer beliebigen Zahl hinzugefügt werden, ohne deren Wert zu ändern, obwohl sie der landläufigen Primzahldefinition genügt, daß sie ganzzahlig nur durch 1 und sich selbst geteilt werden kann. Sie soll im Folgenden mit den echt teilbaren natürlichen Zahlen zusammen die Klasse der Nichtprimzahlen bilden. Bezeichnet σ(x) die Anzahl aller Nichtprimzahlen ≤ x und π(x) die Anzahl aller Primzahlen ≤ x , so gilt
Satz 5.1. Die Anzahl der echt teilbaren natürlichen Zahlen (inclusive der Zahl 1) im abgeschlossenen Intervall [1, x] beträgt mit i0 gemäß Definition 5.4. und der eckigen Klammer nach Definition 5.2.
Bew.: Wie in allen Siebmethoden sollen in der Folge der natürlichen Zahlen {ni}, ni ≤ x, sukzessive alle Vielfachen der Primzahlen pi gestrichen und die Anzahlen σi(x) der echt durch pi teilbaren ermittelt werden, die, beginnend mit der kleinsten Primzahl p1 = 2, noch ungestrichen stehen geblieben sind.
Schritt 0: Streichung der natürlichen Zahl 1 in {ni} als Nichtprimzahl. Es ist σ0(x) = 1.
Schritt 1: In {ni} stehen σ’1(x) = ⎡⎣(x)/(2)⎤⎦ Zahlen , die ohne Rest durch p1 = 2 teilbar sind. Die erste dieser Zahlen ist p1 selbst, welche nicht zu streichen ist, sodaß σ1(x) = ⎡⎣(x)/(p1)⎤⎦ − 1 Streichungen hinzukommen. Zusammen sind nun s1(x) = σ0(x) + σ1(x) = ⎡⎣(x)/(p1)⎤⎦ Zahlen gestrichen.
Schritt 2: In {ni} waren σ’2(x) = ⎡⎣(x)/(p2)⎤⎦ Zahlen ohne Rest durch p2 = 3 teilbar. Davon ist p2 selbst abzuziehen sowie alle geraden Vielfachen von p2, die schon im ersten Schritt erfaßt wurden, nämlich ⎡⎣(x)/(p1p2)⎤⎦ Stück. Somit sind neu zu streichen σ2(x) = ⎡⎣(x)/(p2)⎤⎦ − 1 − ⎡⎣(x)/(p1p2)⎤⎦, sodaß gilt
s2(x) = 2⎲⎳i = 0σi(x) = 1 + ⎡⎣(x)/(p1)⎤⎦ − 1 + ⎡⎣(x)/(p2)⎤⎦ − 1 − ⎡⎣(x)/(p1p2)⎤⎦.
Unter Beachtung der Definitionen 5.2. und 5.3. erkennt man, daß die Behauptung (49↑) bis zum (i0 − 1) − ten Schritt, (i0 − 1) = 2, erfüllt ist. Damit folgt durch Schluß von (i0 − 1) auf i0
Schritt i0: Die kleinste in den ersten (i0 − 1) Schritten nicht gestrichene Zahl, die noch > pi0 − 1 ist, ist die nächste Primzahl pi0. Die Anzahl der in {ni} existenten ganzzahligen Vielfachen von pi0 ist σ’i0(x) = ⎡⎣(x)/(pi0)⎤⎦ − 1. Diese Zahl ist zu vermindern um alle bereits gestrichenen gemeinsamen Vielfachen von pi mit pj , j = 1, 2, …, (i − 1), also ∑i − 1j = 1⎡⎣(x)/(pipj)⎤⎦. Diese letzte Summe ist ihrerseits zu vermindern um die Vielfachen mit 3 gemeinsamen Primfaktoren, also um ∑i0 − 1j1, 2 = 1⎡⎣(x)/(pi0pj1pj2)⎤⎦, j2 > j1, die sonst doppelt gezählt würden. Allgemein ist jede solche Summe mit k Faktoren im Nenner ihrerseits zu vermindern um eine solche mit (k + 1) Nennerfaktoren, solange bis k = i0 erreicht wird:
σi0(x) = 1 + i0⎲⎳i = 1⎛⎝ − 1 + i − 1⎲⎳j = 0( − 1)j ⎲⎳∀k⎡⎣(x)/(piCj, i − 1, k)⎤⎦⎞⎠.
Dies ist die behauptete Beziehung (49↑). Es bleibt lediglich noch darauf hinzuweisen, daß das Verfahren mit dem i0 − ten Schritt abbricht, wenn i0 gemäß Definition 5.4. ermittelt wird, weil spätestens dann alle Nichtprimzahlen ≤ x gestrichen sind; q.e.d.
Zur Veranschaulichung der Gleichung (49↑) mögen folgende Beispiele dienen.
Beispiel 1: x = 122, pi0 = ≺√(122)≻ = 11, also i0 = 5. Somit ergibt sich
σ(x)
=
1 + ⎛⎝⎡⎣(x)/(p1)⎤⎦ − 1⎞⎠ + ⎛⎝⎡⎣(x)/(p2)⎤⎦ − 1 − ⎡⎣(x)/(p1p2)⎤⎦⎞⎠
+ ⎛⎝⎡⎣(x)/(p3)⎤⎦ − 1 − ⎡⎣(x)/(p1p3)⎤⎦ − ⎡⎣(x)/(p2p3)⎤⎦ + ⎡⎣(x)/(p1p2p3)⎤⎦⎞⎠ + s4 + s5
s4
=
⎡⎣(x)/(p4)⎤⎦ − 1 − ⎡⎣(x)/(p1p4)⎤⎦ − ⎡⎣(x)/(p2p4)⎤⎦ − ⎡⎣(x)/(p3p4)⎤⎦ + ⎡⎣(x)/(p1p2p4)⎤⎦ + ⎡⎣(x)/(p1p3p4)⎤⎦ + ⎡⎣(x)/(p2p3p4)⎤⎦
− ⎡⎣(x)/(p1p2p3p4)⎤⎦
s5
=
⎡⎣(x)/(p5)⎤⎦ − 1 − ⎡⎣(x)/(p1p5)⎤⎦ − ⎡⎣(x)/(p2p5)⎤⎦ − ⎡⎣(x)/(p3p5)⎤⎦ − ⎡⎣(x)/(p4p5)⎤⎦ + ⎡⎣(x)/(p1p2p5)⎤⎦ + ⎡⎣(x)/(p1p3p5)⎤⎦
+ ⎡⎣(x)/(p1p4p5)⎤⎦ + ⎡⎣(x)/(p2p3p5)⎤⎦ + ⎡⎣(x)/(p2p4p5)⎤⎦ + ⎡⎣(x)/(p3p4p5)⎤⎦ − ⎡⎣(x)/(p1p2p3p5)⎤⎦
− ⎡⎣(x)/(p1p2p4p5)⎤⎦ − ⎡⎣(x)/(p1p3p4p5)⎤⎦ − ⎡⎣(x)/(p2p3p4p5)⎤⎦ + ⎡⎣(x)/(p1p2p3p4p5)⎤⎦ ,
σ(122)
=
1 + (61 − 1) + (40 − 1 − 20) + (24 − 1 − 12 − 8 + 4)
+ (17 − 1 − 8 − 5 − 3 + 2 + 1 + 1 − 0)
+ (11 − 1 − 5 − 3 − 2 − 1 + 1 + 1 + 0 + ⋯ + 0) = 92.
Daraus folgt nach (48↑) für die Anzahl Primzahlen bis 122 in Übereinstimmung mit Primzahltafeln π(122) = 122 − σ(122) = 30.
Das Beispiel zeigt, daß es zur Berechnung von π(122) reicht, alle Primzahlen
≤ ≺√(122)≻ = 11 = p5 zu kennen, obwohl die größte Primzahl, die bis x = 122 auftritt, p30 = 113 lautet.
≤ ≺√(122)≻ = 11 = p5 zu kennen, obwohl die größte Primzahl, die bis x = 122 auftritt, p30 = 113 lautet.
Beispiel 2: x = 168 ; mittels derselben Formel erhält man σ(168) = 129, also π(168) = 39. Es ist p39 = 167, denn erst ab x = 169 ist p6 = 13 in der Formel für σ(x) zu berücksichtigen. Für konkrete Berechnungen von σ(x) bzw. π(x) für große Zahlen x ist dieses Verfahren natürlich zu aufwändig. Ein möglichst frühzeitiges Erkennen aller Nullsummanden wäre im Interesse einer Aufwandsreduzierung wünschenswert, wie es im Falle des letzten Summanden möglich ist, weil ∀x > 2 gilt pi↓ > x.
Offensichtlich bietet aber die Kenntnis der Gleichung (49↑) prinzipiell eine Möglichkeit, über die Primeigenschaft einer ungeraden Zahl x = 2n + 1 zu entscheiden, indem man Δ = σ(2n + 1) − σ(2n) bildet. Voraussetzung dafür ist die Kenntnis aller Primzahlen ≤ pi0 = ≺√(2n + 1)≻. Ergibt sich Δ = 1, so ist x teilbar; im Falle Δ = 0 ist x Primzahl. Es ist hierzu keinerlei Kenntnis über Primzahlen > pi0 erforderlich. Berechnet man zusätzlich σ(2n + 3), so erfährt man, ob ein Primzahlzwilling vorliegt. Gilt Δ2 = σ(2n + 3) − σ(2n + 1) = 2, so muß x = 2n + 3 neben 2n + 2 teilbar sein, für Δ2 = 1 ist x2 = 2n + 3 Primzahl. D.h. für Δ = Δ2 = 1 gilt {2n + 1, 2n + 3} = Primzahlzwilling. Auch hierzu zwei simple Beispiele aus dem Intervall p23 = 25 < x < p24 = 49. Wegen i0 = 3 genügt die Betrachtung der Formel aus Beispiel 1 ohne s4 und s5.
Beispiel 3: 2n = 28 liefert σ(2n) = 19, π(2n) = 9, σ(2n + 1) = 19, π(2n + 1) = 10. Also ist 29 eine Primzahl. Wegen σ(2n + 3) = 20, π(2n + 3) = 11 ist auch 31 Primzahl, also ist {29, 31} ein Primzahlzwilling.
Beispiel 4: 2n = 40 liefert σ(40) = 28, π(40) = 12, σ(41) = 28, π(41) = 13, σ(43) = 29, π(43) = 14, also ist auch {41, 43} Zwilling.
5.3 Ein Satz zur Primzahlverteilung
Satz 5.2. Sei n eine beliebige natürliche Zahl. Dann gibt es ∀n < ∞ kein links offenes Intervall
das nicht mindestens 2 Primzahlen enthält.
Es gilt sogar für die Anzahl der Primzahlen in ηn
Bew.: Für n = 1 enthält das Intervall η1 = (1, 4] nur 2 innere Zahlen, die Primzahlen 2 und 3. Die Intervallränder sind konstruktionsbedingt stets nichtprim. Nach (49↑) ergibt sich die Anzahl von Nichtprimzahlen im Intervall (50↑) zu
σ(ηn) = σ((n + 1)2) − σ(n2) = 1 + i’0⎲⎳i = 1⎛⎝ − 1 + i − 1⎲⎳j = 0( − 1)j ⎲⎳∀k⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦⎞⎠
Darin bedeuten i0, i’0 die Indizes aus
Aus (52↑) folgt
σ(ηn) = i0⎲⎳i = 1i − 1⎲⎳j = 0( − 1)j ⎲⎳∀k⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦ − i0⎲⎳i = 1i − 1⎲⎳j = 0( − 1)j ⎲⎳∀k⎡⎣(n2)/(piCj, i − 1, k)⎤⎦ + D
mit
Es ist
D = \Biggr{0 für i0 = i’0, d.h. n + 1 ≠ Primzahl, \atop − 1 + i0⎲⎳j = 0( − 1)j ⎲⎳∀k⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦ sonst.
Da n und (n + 1) benachbarte natürliche Zahlen sind, kann i’0 > i0 nur gelten, wenn (n + 1) = pi0 + 1 = pi’0 selbst Primzahl ist. Für den Fall, daß (n + 1) nichtprim ist, muß daher gelten i’0 = i0, woraus D = 0 folgt. Dann lassen sich die Summen vollständig zusammenfassen:
(55) σ(ηn) = i0⎲⎳i = 1i − 1⎲⎳j = 0( − 1)j ⎲⎳∀k⎛⎝⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦ − ⎡⎣(n2)/(piCj, i − 1, k)⎤⎦⎞⎠.
Am Schluß des Beweises von Satz 5.1. wurde darauf hingewiesen, daß im Ausdruck für σ(x) die Summe über i automatisch bei i0 abbricht. Läßt man nun im Ausdruck σ(ηn) auch für σ(n2) die Summe über i bis i’0 laufen wie bei σ((n + 1)2), so begeht man keinen Fehler, weil dadurch der Wert weder für σ(n2) noch für σ(ηn) geändert wird. Ersetzt man in (55↑) i0 durch i’0, so stellt diese Gleichung den allgemein gültigen Ausdruck für σ(ηn) dar. Wir lassen daher im Folgenden einfach D weg und interpretieren das i0 als i’0. Durch Einführung der Summationsschrittweite 2 (in Zeichen: ∑i − 1j = 0(2)⋯) lassen sich Terme mit gleichen Vorzeichen in endlichen Summen zusammenfassen:
(56)
σ(ηn)
=
i0⎲⎳i = 1\Biggl{i − 1⎲⎳j = 0(2) ⎲⎳∀k⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦ − i − 1⎲⎳j = 1(2) ⎲⎳∀k⎡⎣((n + 1)2)/(piCj, i − 1, k)⎤⎦
− i − 1⎲⎳j = 0(2) ⎲⎳∀k⎡⎣(n2)/(piCj, i − 1, k)⎤⎦ + i − 1⎲⎳j = 1(2) ⎲⎳∀k⎡⎣(n2)/(piCj, i − 1, k)⎤⎦\Biggr}.
Diese Gleichung sollte nun nach beiden Seiten abgeschätzt werden. Mit Hilfe von (40↑) schätzt man ab ⎡⎣((n + 1)2)/(pC)⎤⎦ − ⎡⎣(n2)/(pC)⎤⎦ ≥ ⎡⎣(2n + 1)/(pC)⎤⎦ und ⎡⎣((n + 1)2)/(pC)⎤⎦ − ⎡⎣(n2)/(pC)⎤⎦ ≤ − ⎡⎣ − (2n + 1)/(pC)⎤⎦, letzteres folgt durch Multiplikation mit ( − 1) aus ⎡⎣(n2)/(pC)⎤⎦ − ⎡⎣((n + 1)2)/(pC)⎤⎦ ≥ ⎡⎣ − (2n + 1)/(pC)⎤⎦. Die Zusammenfassung beider Ungleichungen ergibt
und
In (56↑) werden nun die Terme mit gleichem Summationsschritt zusammengefaßt sowie der 1. und 3. Term mittels (57↑), der 2. und 4. Term mittels (58↑) abgeschätzt:
(59)
σ(ηn)
≥
i0⎲⎳i = 1⎛⎝i − 1⎲⎳j = 0(2) ⎲⎳∀k⎡⎣(2n + 1)/(piCj, i − 1, k)⎤⎦ + i − 1⎲⎳j = 1(2) ⎲⎳∀k⎡⎣ − (2n + 1)/(piCj, i − 1, k)⎤⎦⎞⎠
=
i0⎲⎳i = 1i − 1⎲⎳j = 0 ⎲⎳∀k⎡⎣( − 1)j(2n + 1)/(piCj, i − 1, k)⎤⎦
sowie
(60)
σ(ηn)
≤
i0⎲⎳i = 1⎛⎝i − 1⎲⎳j = 0(2) ⎲⎳∀k − ⎡⎣ − (2n + 1)/(piCj, i − 1, k)⎤⎦ − i − 1⎲⎳j = 1(2) ⎲⎳∀k⎡⎣(2n + 1)/(piCj, i − 1, k)⎤⎦⎞⎠
= −
i0⎲⎳i = 1i − 1⎲⎳j = 0 ⎲⎳∀k⎡⎣( − 1)j + 1(2n + 1)/(piCj, i − 1, k)⎤⎦.
Aus der Vereinigung von (59↑) und (60↑) folgt nach Abschätzung gemäß (39↑) - imFalle von (60↑) mit umgekehrtem Vorzeichen -
(61) i0⎲⎳i = 1i − 1⎲⎳j = 0 ⎲⎳∀k( − 1)j(2n + 1)/(piCj, i − 1, k) ≤ σ(ηn) ≤ i0⎲⎳i = 1i − 1⎲⎳j = 0 ⎲⎳∀k( − 1)j(2n + 1)/(piCj, i − 1, k) ,
also die Gleichheit. Durch Einsetzen von (46↑) ergibt sich
(62) σ(ηn) = (2n + 1)i0⎲⎳i = 1p − 1ii − 1⎲⎳j = 0 ⎲⎳∀k(( − 1)j)/(Cj, i − 1, k) = (2n + 1)i0⎲⎳i = 1p − 1ii − 1∏j = 1⎛⎝1 − (1)/(pj)⎞⎠.
Darin gilt nach Definition ∏0j = 1⎛⎝1 − (1)/(pj)⎞⎠ = 1. Wegen (48↑), angewendet auf das Intervall ηn mit der Breite bn = (n + 1)2 − n2 = 2n + 1, gilt dann
Ersetzt man − p − 1i = ( − 1 + (1 − p − 1i)) und multipliziert dies aus (Umordnungen in endlichen Produkten sind erlaubt) , so heben sich Summanden paarweise auf. Man erhält
(64) Sn: = (π(ηn))/(2n + 1) = 1 + i0⎲⎳i = 1⎛⎝i∏j = 1⎛⎝1 − (1)/(pj)⎞⎠ − i − 1∏j = 1⎛⎝1 − (1)/(pj)⎞⎠⎞⎠ = i0∏j = 1⎛⎝1 − (1)/(pj)⎞⎠.
Diese Formel liefert bei numerischer Auswertung für kleine Werte von n, pi0 = ≺n + 1≻ die reale Anzahl von Primzahlen im n-ten Quadratintervall mit einem maximalen Fehler von ±2 für n ≤ 40 bei Verwendung ganzzahlig abgerundeter Werte. Auch die daraus bestimmte Anzahl von Primzahlen ≤ x, π(x) = ∑n0n = 0π(ηn), liefert, s. Tab. 5.1., sinnvolle Werte:
| n0 | 10 | 20 | 30 | 40 |
| π((n0 + 1)2) | 26 | 80 | 161 | 266 |
| Realwert | 30 | 85 | 162 | 263 |
Wir bilden nun lnSn, spalten den 1. Term ab und entwickeln dann den Logarithmus in eine Potenzreihe:
(65)
lnSn
=
lni0∏j = 1⎛⎝1 − (1)/(pj)⎞⎠ = ln(1)/(2) + i0⎲⎳j = 2ln⎛⎝1 − (1)/(pj)⎞⎠ = ln(1)/(2) − i0⎲⎳j = 2∞⎲⎳ν = 1(1)/(νpνj)
=
ln(1)/(2) − i0⎲⎳j = 2(1)/(pj) − i0⎲⎳j = 2∞⎲⎳ν = 2(1)/(νpνj).
Darin ist A = − ∑i0j = 2∑∞ν = 2(1)/(νpνj) = const., denn wegen ν ≥ 2 ist A eine absolut konvergente Reihe. Aus der Literatur [1], p.343, Satz 5, entnehmen wir die Aussage
worin c = const. und O⎛⎝(1)/(lnpi0)⎞⎠ den Fehlerterm bezeichnet. Der Wert lnlnx = 0 wird für x = e angenommen, lnlnp1 = lnln2 = − 0, 3665129… < 0, lnln3 = 0, 094047827…, ln3 = 1, 098612289… . Da in (65↑) j = 2, …, i0 läuft, haben wir die Belegung der Konstanten etwas zu modifizieren. Um den Wert von lnlnpi0 benutzen zu können, haben wir davon lnln3 abzuziehen. So erhält man schließlich
sowie durch Exponentiation
mit A’ = (ln3)e − c + A − O(1 ⁄ lnpi0). Dies ist die Aussage des Gauß’schen Primzahlsatzes für Quadratintervalle. Für 0≃A − c − O(1 ⁄ lnpi0) wird A’≃ln3.
Wenn aber die Primzahlverteilung über jedem Quadratintervall diesem logarithmi-schen Gesetz gehorcht, gilt sie für jedes beliebige größere Intervall, also auch für (1, x], wie es der Gauß’sche Primzahlsatz verlangt: π(x) = A’’⎛⎝(x)/(lnx)⎞⎠ln3, denn 2lnpi0 = lnp2i0≃ln(n + 1)2 = lnx. Die Formel π(x) = ⎛⎝(x)/(lnx)⎞⎠ gibt im allgemeinen Werte, die um 5…10% zu niedrig liegen. Der Faktor ln3 vergrößert sie um 9,86% , sodaß wohl A’’ < 1, aber nahe bei 1, anzunehmen ist.
Wir haben hier das logarithmische Verteilungsgesetz für Quadratintervalle abgeleitet aus einer (ziemlich koplizierten) exakten Formel, daraus auf seine allgemeine Gültigkeit geschlossen und den Gauß’schen Satz als Approximation erhalten; q.e.d.
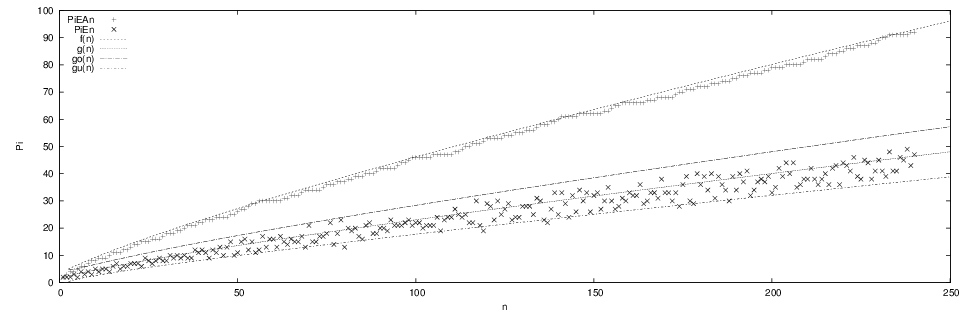
Die Abb. 5.1. zeigt ∀n ≤ 240 die Anzahlen π(ηn) = PiEn und π(ηA, n) = π(2n + 1) = (A’(2n + 1))/(ln(n + 1)) =PiEAn sowie die gemäß (71↓) streuenden Funktionen πs(ηn) = π(ηn)(1 + δ) mit δ = 0 für den Mittelwert g(n), δ = + (A’)/(ln(n + 1)) als obere Schranke go(n), δ = − (A’)/(ln(n + 1)) als untere Schranke gu(n). Der im Mittel stetige Anstieg ist deutlich zu erkennen, ebenso daß im Anfangsintervall gleicher Größe ηA, n: = [0, 2n + 1] der Gauß’sche Satz π(ηA, n) = (A’(2n + 1))/(ln(n + 1)) ≈ 2π(ηn) ergibt.
\endsamepage \endlandscape \newpage
5.4 Vertrauensgrenzen des Verteilungssatzes
Nach (68↑) haben wir mit pi0 = ≺n + 1≻≅n + 1 als Wahrscheinlichkeit W aus mittlerer Anzahl π(ηn) der Primzahlen im Intervall ηn mit der Breite bn = 2n + 1 erhalten:
Der Kehrwert Ln = (1)/(W) = (bn)/(π(ηn)) kann als mittlerer Platzbedarf einer Primzahl in ηn gedeutet werden. Wir bestimmen stattdessen den halben Platzbedarf (1)/(2)L’n eines Primzahlpaares. Die Wahrscheinlichkeit, daß 2 Zahlen Primzahlen in ηn sind, wird durch ihr Wahrscheinlichkeitsprodukt Wges. = Wp1Wp2 = W2 gegeben. Dann ist die Streubreite für eine Primzahl in ηn
Da p1 = 2 die kleinste Primzahl ist, kann (außer zwischen p1 und p2 = 3) der minimale Primzahlabstand nicht kleiner als 2 sein. Der Abstand zwischen zwei benachbarten Primzahlen ist kleiner als das zugehörige bn, deshalb gilt 2 ≤ pi + 1 − pi < bn.
Deshalb erhalten wir für die in ηn streuende Anzahl von Primzahlen
(71) πs(ηn) = bnW±Sn = (A’⎛⎝n + (1)/(2)⎞⎠)/(ln(n + 1))±(A’2⎛⎝n + (1)/(2)⎞⎠)/(ln2(n + 1)) = (A’⎛⎝n + (1)/(2)⎞⎠)/(ln(n + 1))⎛⎝1±(A’)/(ln(n + 1))⎞⎠.
bzw. πs(x) = (A’x)/(lnx)±(2A’2x)/(ln2x) . Dieser Toleranzbereich ist realistischer als die willkürliche Annahme πs(x) = (A’x)/(lnx)(1±0, 2) und beschreibt die Realität gut, s. Abb. 5.1. und
Tab. 5.2.:
Tab. 5.2.:
| n | 1 | 10 | 100 | 150 | 300 | 400 | 103 | 104 | 105 | 106 |
| π(ηn) | 2,29 | 4,4 | 23,1 | 31,9 | 55,8 | 70,8 | 154 | 1151 | 9207 | 76725,4 |
| Ln | 0,86 | 10,2 | 37,9 | 44,8 | 58,0 | 64,0 | 85,0 | 151,0 | 235,9 | 339,7 |
| ±(2n + 1)/(Ln) | 3,5 | 2,05 | 5,30 | 6,72 | 10,4 | 12,5 | 23,6 | 132,5 | 847,7 | 5886,9 |
Größere Schwankungen sind möglich: Der wirkliche Extremfall, daß die erste Primzahl am unteren, die zweite am oberen Intervallrand liegt, könnte schlimmstenfalls das Doppelte vom mittleren Primzahlabstand erbringen und statistische “Ausreißer” erklären.
Bezeichnet Δπmax(x) die in der weiteren Umgebung von x auftretenden maximalen Primzahlabstände, so gibt Tab 5.3. den Vergleich mit den Primzahlabständen gemäß (70↑ ):
| x | 10 | 102 | 103 | 104 | 105 | 8,4⋅105 |
| Δπmax(x) | 4 | 14 | 20 | 36 | 54 | 100 |
| (ln2x)/(2A’2) | 2,36 | 9,44 | 21,23 | 37,75 | 58,98 | 82,81 |
Es wurde mit A’ = 1, 06 gerechnet.
6 Ein falscher Satz
In der Literatur findet man seit langer Zeit die Behauptung, man könne “beliebig große primzahlfreie Intervalle” konstruieren (s. z.B. [1], p. 22 Zeile 12) und die Frage nach einer oberen Schranke für den Abstand benachbarter Primzahlen sei sinnlos. Zum Beweis konstruiert man die Intervalle [n!±2, n!±n] , die primzahlfreie Intervalle der Mindestlänge (n − 1) darstellen, und läßt n → ∞ laufen. Von jeder endlichen Zahl n! − 1 rückwärts gezählt, steht natürlich kein beliebig ( = ∞) großes primzahlfreies Intervall zur Verfügung. Von n! + 1 nach “oben” gezählt, steht zunächst nur das endliche primzahlfreie Intervall der Länge n − 1 bereit. ( De facto kann das primzahlfreie Intervall auch doppelt so groß sein!) Die angegebene Konstruktion beweist in der Tat nur, daß “im unendlich fernen Punkt” selbst genau ein beliebig großes primzahlfreies Intervall gedacht werden kann. Dieser “Punkt“ ist aber singulär und zugleich der einzige Häufungspunkt der Primzahlen. Der Satz ist also falsch.
Wegen Satz 5.2. gibt es kein primzahlfreies Quadratintervall ηn = (n2, (n + 1)2]. Daraus folgt, daß der maximale Abstand zwischen benachbarten Primzahlen < 2n für jede vorgelegte Zahl x = n2 ist, d.h. Δmax = pi + 1 − pi < 2[√(pi + 1)]. Man kann sogar den Mittelwert Δmax, M sowie obere und untere Schranken dazu aus dem logarithmischen Verteilungsgesetz über Quadratintervallen ableiten. Wir werden in den folgenden Kapiteln dieser Frage nochmals begegnen. Solche Angaben werden natürlich n-abhängig sein.
Beim Vergleich verschieden mächtiger Mengen muß etwas mehr Sorgfalt aufgewendet werden. Eine Zahl m = pn↓ oder m = n! gehört zur Potenzordnung n, da sie n Faktoren enthält. Das Quadratintervall (√(m)2, (√(m) + 1)2], in dem m liegt, hat die Potenzordnung 2 < n und die lineare Breite b = 2√(m) + 1 = 1 + 2√(n!)≫n − 1 = primzahlfreies Intervall, welches eine lineare Mannigfaltigkeit darstellt, das schon die umgebende Mannigfaltigkeit 2. Ordnung (Quadratintervall) nicht auszufüllen vermag. Dies dürfte die Ursache des Trugschlusses im angeführten Satz von der Konstruierbarkeit “beliebig großer” primzahlfreier Intervalle gewesen sein.
Obwohl also zu jeder beliebig gewählten natürlichen Zahl n<∞ eine natürliche Zahl n’=n!+1konstruierbar ist, der ein primzahlfreies Intervall der Mindestlänge n-1 folgt, gibt es keine natürliche Zahl, der ein beliebig langes primzahlfreies Intervall folgen kann.
7 Zur Verteilung von Primzahlzwillingen
Die Primzahlen sind bezüglich der Multiplikation statistisch unabhängig, denn eine jede Primzahl p enthält als Teiler nur 1 und p und ist selbst kein Teiler irgend einer anderen Primzahl. Primzahlen sind sozusagen die Ein-heiten der Produktmengen. Es ist daher legitim, die Zwillingsbedingung pi + 1 = pi + 2 zu kombinieren mit dem Primzahlverteilungsgesetz über einem Quadratintervall ηn oder einem größeren Intervall. Zuvor stellen wir noch fest, daß ein Primzahlzwilling mit pi > 3 niemals eine Quadratzahl umgreifen kann. Es müssen daher - außer {p2 = 3, p3 = 5} mit 22 in der Mitte - die beiden Partner eines beliebigen Primzahlzwillings > 5 stets vollständig ein und demselben Quadratintervall angehören.
Bew.: x2 − 1 = (x + 1)(x − 1) ist ∀i > 2 eine stets teilbare Zahl, deshalb kann höchstens x2 + 1 Primzahl sein, sodaß zwar ein Primzahlzwilling am Anfang eines Quadratintervalls, aber vollständig darin stehen kann, wenn x geradzahlig ist. Ist x ungerade, so stehen 2 teilbare Zahlen nebeneinander: x2und (x − 1)(x + 1), sodaß ebenso nur der Anfang x2 + 1 des größeren Quadratintervalls für die Bildung eines Primzahlzwillings in Betracht kommt; q.e.d.
Für die Primzahldichte über einem Quadratintervall (wahrscheinlichster oder Mittelwert) ergab sich in (68↑)
mit pi0 = ≺n + 1≻, ηn = (n2, (n + 1)2]. Ein Primzahlzwilling ist gekennzeichnet durch die Annahme des geringstmöglichen Primzahlabstandes 2, also pi + 1 = pi + 2. Da pi, pi + 1 im gleichen Quadratintervall liegen müssen, wird ihre Wahrscheinlichkeit durch dasselbe pi0 bestimmt. Es darf also die Zwillingswahrscheinlichkeitsverteilung als Wz = WiWi + 1 = W2 angesetzt werden. Bezeichnet π2(ηn) die mittlere oder wahrscheinliche Anzahl von Primzahlzwillingen in ηn, so kann geschrieben werden
Wz = (π2(ηn))/(2n + 1) = (A’’2ln23)/(4ln2pi0)
oder
Diese Funktion ist in Abb. 7.1. zwischen die Punkte der numerisch bestimmten Primzahlzwillings-Anzahlen je ηn ∀n ≤ 915 eingezeichnet und zeigt eine gute Approximation an. Es wurde A’ = A’’ln(3) = 1, 06 benutzt.
Satz 7.1. Die mittlere Anzahl von Primzahlzwillingen im Quadratintervall ηn steigt gemäß (73↑) mit n monoton an und wächst für n → ∞ über alle Schranken. Die integrale Anzahl der Primzahlzwillinge wächst dann natürlich erst recht über alle Schranken.
Bew.: Aus der Divergenz des Ausdrucks y = (√(x − 1 ⁄ 2))/(lnx) (der Logarithmus wächst schwächer als jede Potenzfunktion xν mit ν > 0 ) folgt mit x = n + 1 auch die Divergenz von y2 = (n + 1 ⁄ 2)/(ln2(n + 1)), daran ändert auch der konstante Faktor (ln23)/(2) nichts; q.e.d.
Dies Ergebnis ist insofern erstaunlich, als im Anfangsbereich (n ≤ 122) primzahlleere Quadratintervalle existieren für n = {9, 19, 26, 27, 30, 34, 39, 49, 53, 77, 122}, darunter sogar 2 benachbarte Quadratintervalle. Fragt man aber nach dem größten Wert von n, oberhalb dessen ein vorgegebener ganzzahliger Wert von π2(ηn) nicht mehr unterschritten wird, so ergibt sich mit π2(ηn, max) nach (73↑) aus der Abb.7.1. folgende Tabelle Tab.7.1.:
| nmax | 122 | 213 | 502 | 545 | 829 |
| π2(ηn) | 0 | 1 | 2 | 3 | 4 |
| π2(ηn, max) | 3,19 | 4,47 | 7,84 | 8,29 | 11,09 |
\psfragPi2
π2
\endlandscape \newpage
Das wirft die Frage nach der Streubreite um die mittlere theoretische Häufigkeit π2(ηn) auf. Benutzt man in (68↑) für A’ = 1, 06 anstelle von A’’ln3 = A’’⋅1, 0986123…, so stimmen der Mittelwert
die obere Schranke
und die untere Schranke
für n < 1000 befriedigend mit der Realität überein. Durch Quadrieren der Wahrscheinlichkeitsausdrücke ergibt sich damit für Primzahlzwillinge
Während der Mittelwert gut liegt, ist die reale Abweichung vom Mittelwert etwa doppelt so groß. Dieser Mangel wird überwunden, wenn man statt der willkürlichen Streufaktoren 0,8 und 1,2 die besser begründete mittlere Abweichung gemäß (71↑) einführt.
Wir betrachten 2 Primzahlzwillinge mit der Gesamtwahrscheinlichkeit Wges. = Wz1Wz2 = W2s, weil für genügend große n der Zwillingsabstand < bn ist. Für den einzelnen Primzahlzwilling verdoppeln wir wieder den streuenden Anteil und erhalten
(80)
π2, s(ηn)
=
(2n + 1)⎛⎝(A’)/(2ln(n + 1))⎞⎠2⎛⎝1 + 2⎛⎝4⎛⎝(A’)/(2ln(n + 1))⎞⎠2±4(A’)/(2ln(n + 1))⎞⎠⎞⎠
=
(2n + 1)⎛⎝(A’)/(2ln(n + 1))⎞⎠2(1 + δ2),
Darin sind die Streufaktoren δ2 = 0 für den Mittelwert, für die obere und untere Schranke
Die 3 Funktionen sind in Abb. 7.1. neben den Werten des numerischen Experiments eingezeichnet; sie beschreiben die Realität hinreichend gut. Die Tab. 7.2. zeigt, daß die nach (80↑) berechnete gesamte Streubreite sich oberhalb eines Schwellwertes über die n-Achse erhebt und für große n nahezu symmetrisch wird, während bei kleinen n deutlich δ2, + > δ2, − gilt. Tab. 7.2.:
| n | 1 | 10 | 102 | 103 | 104 | 105 | 106 |
| π2(ηn) | 1,75 | 1,03 | 2,65 | 11,78 | 66,23 | 423,85 | 2943,39 |
| π2(ηn)δ2, + | 11,19 | 2,14 | 4,01 | 15,68 | 82,32 | 505,23 | 3411,39 |
| π2(ηn)δ2, − | 0,49 | 0,32 | 1,57 | 8,45 | 51,86 | 349,25 | 2510,71 |
8 Primzahlvierlinge
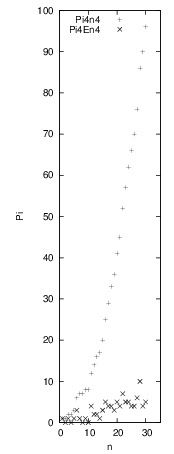
Wegen der statistischen Unabhängigkeit aller Primzahlen voneinander sollte man annehmen, daß auch die Vierlingsmenge unendlich ist. Dem steht entgegen, daß es offenbar für kleinere Werte von n nur wenige Quadratintervalle gibt, die einen Vierling enthalten. Da nun die Vierlinge bezüglich ihrer Wahrscheinlichkeitsfunktion eine Menge der 4. Potenzordnung darstellen, seien in Abb. 8.1. die Anzahl der Vierlinge ≤ n4 , π4(n4), und die Vierlingsanzahl im Intervall η4, n: = (n4, (n + 1)4] , π4(η4, n), über n ≤ 30 dargestellt. Offensichtlich ist das Intervall η4, 10 das größte vierlingsfreie Intervall, im Intervall η4, 14 tritt letztmalig nur 1 Vierling auf. Diese Tatsache steht im Einklang mit unserem statistischen Ansatz, nach dem zur Intervallbreite b4, n = 4n3 + 6n2 + 4n + 1
als mittlere Primzahlvierlingsanzahl
≤ (n + 1)4 zu erwarten ist.
≤ (n + 1)4 zu erwarten ist.
Satz 8.1. Da die Anzahl biquadrati-scher Intervalle mit mehr als 1 Vierling nach oben offen ist, muß es auch unendlich viele Primzahlvierlinge geben.
Der Satz bleibt hier als Vermutung stehen. Ob es ein n0 gibt, sodaß ∀n > n0 jedes Quadratintervall η2, n mindestens einen Primzahlvierling enthält, ist damit noch nicht entschieden; es ist aber nahe gelegt. Ein solches n0 müßte aber deutlich über n = 1000 liegen, denn oberhalb n = 900 gibt es noch primzahlvierlingsfreie Quadratintervalle. Unterhalb n = 914 gibt es insgesamt 96 Primzahlvierlinge.
9 Zur Goldbach-Hypothese
Christian Goldbach (1690-1764) vermutete in einem Brief an Leonhard Euler, daß jede gerade Zahl ≥ 6 als Summe aus genau 2 ungeraden Primzahlen dargestellt werden kann. Wir wollen sie in den etwas schärferen Satz fassen:
Satz 9.1. a) Jede gerade Zahl 2m ≥ 8, mϵℕ, kann als Summe aus genau 2 voneinander verschiedenen ungeraden Primzahlen dargestellt werden. Zusätzlich
existiert ∀ Primzahlen p eine Darstellung 2m = 2p.
existiert ∀ Primzahlen p eine Darstellung 2m = 2p.
b) Die Darstellung 2m = pi + pj, pi ≠ pj, ist im allgemeinen vieldeutig; eindeutig ist sie nur für einige relativ kleine Werte von 2m ≤ 2m0 = 12, (wenn pi = pj mit gewertet wird). Die Vielfachheit v2m der Goldbachpaar-Darstellungen von 2m erfüllt
Bew.: Der Beweis soll auf probabilistischer Grundlage geführt werden. Das ist zulässig, da die Gültigkeit der Verteilungsfunktion A’ ⁄ lnx für jedes Intervall (1, x] aus seiner Gültigkeit ∀ηn folgt, also bereits gezeigt ist, und alle Primzahlen als statistisch unabhängig erwiesen sind.
Die Summe aus 2 ungeraden Primzahlen
(85) pi + pj = 2m
ist stets geradzahlig. Aus der Forderung pi ≠ pj folgt dann o.B.d.A. pi < pj sowie die Existenz einer Zahl Δ , sodaß pi = m − Δ und pj = m + Δ gilt. Wir betrachten nun ein Quadratintervall ηn = (n2, (n + 1)2] mit n ≥ n0, sodaß auch noch jede gerade Zahl aus ηn − 1 oberhalb m und das Intervall η’A, n: = (0, 4n] vollständig unterhalb m liegt. Die Breite bA von η’A, n ist gleich der Summe der Breiten von ηn − 1 und ηn , also bA = (2n + 1) + (2n − 1) = 4n. Daher gilt n0 = 7. Für alle geraden Zahlen unterhalb dieser Größe prüfen wir Satz 9.1. explizit numerisch:
4=2+2; 6=3+3; 8=3+5; 10=3+7=5+5; 12=5+7; 14=3+11=7+7; 16=3+13=5+11; 18=5+13=7+11; 20=3+17=7+13; 22=3+19=5+17=11+11; 24=5+19=7+17=11+13; 26=3+23=7+19=13+13; 28=5+23=11+17; 30=7+23=11+19; 32=3+29=13+19;
34=3+31=5+29=11+23=17+17; 36=5+31=7+29=13+23=17+19.
34=3+31=5+29=11+23=17+17; 36=5+31=7+29=13+23=17+19.
Es sei hier bemerkt, daß in der Regel schon mindestens ein Goldbachpaar auftritt mit pjϵηn, in einigen Fällen wird aber das erste Goldbachpaar erst mit pjϵηn − 1 gefunden. Für sehr große n kann nicht ausgeschlossen werden, daß das erste pj, das ein Goldbachpaar bildet, noch kleiner ist. Das stört aber unsere Betrachtung nicht, da zur Bestimmung der Vielfachheit v der möglichen Goldbachpaar-Darstellungen alle pj mit m ≤ pj < (n + 1)2 zu berücksichtigen sind und hinreichend viele Quadratintervalle im Intervall (m, (n + 1)2] existieren.
Die Wahrscheinlichkeit Wg, daß die erste Primzahl in (85↑) piϵηA, n und die zweite pjϵηn erfüllt, ist durch das Produkt ihrer entsprechenden Wahrscheinlichkeiten definiert. Wegen
gilt für das Paar {pi, pj}
(87) Wg = 2W2j.
Für die einzelne Zahl 2m haben wir wieder den streuenden Anteil zu verdoppeln, sodaß wir für die streuende Anzahl von Goldbachpaar-Darstellungen zahlenmäßig das Doppelte der Primzahlzwillingsanzahl in ηn gemäß (80↑) erhalten:
wie in Satz 9.1.b behauptet wurde, wobei v2m = πg(2m) gesetzt ist; q.e.d.
Beide Ausdrücke wachsen aber mit m über alle Schranken. Wegen des Faktors 2 erhebt sich jedoch die Funktion πg(2m) inclusive ihrem Streubereich schneller über die Anzahl “1” . Die Abb. 9.1. zeigt den Anfangsbereich von πg(2m) im numerischen Experiment zusammen mit den theoretisch ermittelten Werten für 2m ≤ 330.
Satz 9.2. Unter Goldbachpaaren versteht man im allgemeinen nur Paare ungerader Primzahlen, deren Summe eine gerade Zahl 2m ergibt. Läßt man auch die kleinste Primzahl p1 = 2 als Paarpartner zu, so können auch alle ungeraden Zahlen, die um 2 größer sind als eine Primzahl, als Summe aus genau 2 Primzahlen dargestellt werden. Das sind zwar unendlich viele ungerade Zahlen, genau so viele wie es Primzahlen gibt, aber bei weitem nicht alle. Es gibt sogar unendlich viele Primzahlen, die als Summe aus genau einer ungeraden Primzahl und p1 = 2 dargestellt werden können. Diese ungeraden Zahlen sind der kleinere Partner eines jeden Primzahlzwillings, von denen wir zeigen konnten, daß ihre Anzahl unendlich ist.
Satz 9.3. Die Zahl 5 ist die einzige ungerade unberührbare Zahl.
Man bezeichnet eine natürliche Zahl z als unberührbar, wenn es keine natürliche Zahl x gibt, deren echte Teilersumme σ*(x) = z ist.
Man bezeichnet eine natürliche Zahl z als unberührbar, wenn es keine natürliche Zahl x gibt, deren echte Teilersumme σ*(x) = z ist.
Bew.: Behauptung und Beweis sind angelehnt an Aufgabe 48 b in [1], p. 327 und 336. Die Behauptung folgt aus dem Goldbachtheorem in der Fassung von Satz 9.1.a. Jede ungerade natürliche Zahl z > 8 hat eine Darstellung z = 1 + 2n mit 2n ≥ 8 . Jede gerade Zahl 2n ≥ 8 hat mindestens eine Darstellung 2n = p + q mit den Primzahlen p ≠ q . Die Zahl x = p⋅q hat die Summe echter Teiler σ*(x) = 1 + p + q = 1 + 2n = z. Die Zahlen z = 3 und z = 7 sind berührbar (x = 4 bzw. x = 8); q.e.d.
Literatur
[1] H. Scheid, Zahlentheorie, Mannheim, Wien, Zürich: BI-Wiss.-Verl., 1991
Danksagung
Für die Wartung und Systembetreuung meines PC danke ich Christian Schmidt-Gütter und für Unterstützung bei der Arbeit mit LaTeX und gnuplot Susanne Gütter.